fisheye lenses

panoramic cameras

rendering for the imax dome

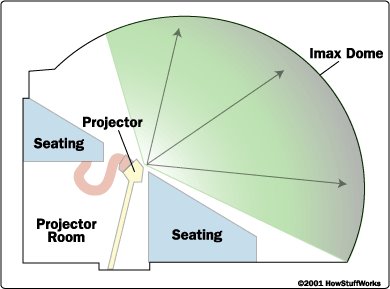
rendering for virtual reality

photorealistic rendering

• flat and boring bokeh

photorealistic rendering

• interesting bokeh, distortion, and vignetting to match plate

approximate lens systems with simple polynomial

• collapse complicated ray tracing
• simple function evaluations $\mathbf{A} = P_a(\mathbf{S})$ and $\mathbf{O} = P_o(\mathbf{S})$

optics use polynomials to ray trace

• approximate ray tracing using polynomials for lens designers [ZHB10]
• and analyse error in that domain directly

all based on Taylor expansion

• scary formulas for analytic differentiation required!
• not precise in outer rims [HD14]
  • use Taylor configuration, optimise coefficients

fisheye lenses

• precision in periphery is important!
• current lens connections (for light tracing)
  • sample outer pupil uniformly
  • have terrible performance

• parametrise the light fields for fisheyes
  • no plane/plane 180-degree limit

• parametrise the light fields for fisheyes
  • no plane/plane 180-degree limit
• sparse fitting of high-degree polynomials
  • use orthogonal matching pursuit (OMP)
  • enables trade-off between approximation error and evaluation speed

• parametrise the light fields for fisheyes
  • no plane/plane 180-degree limit
• sparse fitting of high-degree polynomials
  • use orthogonal matching pursuit (OMP)
  • enables trade-off between approximation error and evaluation speed
• aperture sampling for light tracing
  • enable the use in bidirectional path tracing etc.

• parametrise the light fields for fisheyes
  • no plane/plane 180-degree limit
• sparse fitting of high-degree polynomials
  • use orthogonal matching pursuit (OMP)
  • enables trade-off between approximation error and evaluation speed
• aperture sampling for light tracing
  • enable the use in bidirectional path tracing etc.
• fast GPU preview rendering implementation

• plane/plane on sensor
• plane/plane on aperture
• hemi-sphere/hemi-sphere on outer pupil

hemi-sphere/hemi-sphere on outer pupil

• need to specify tangent frame for $dx, dy$
• avoid the singularity in interesting regions on the outer pupil

finding a polynomial

• polynomial consists of these terms: $$c \cdot \underbrace{x_s^{d_{0}} y_s^{d_{1}} dx_s^{d_{2}} dy_s^{d_{3}} \lambda_s^{d_{4}}}_{=:T_t} \text{ with degree } \sum_{i=0}^4 d_{i} \le d$$
• find most closely matching polynomial for given set of ray traced reference samples
  • linear problem, Galerkin projection of function $\mathbf{O} = P_o(\mathbf{S})$ to

    $$\mathbf{O} \approx \hat\Phi \cdot \mathbf{c}$$ with

    $$\hat\Phi = \left(\begin{array}{ccccc} T_1 & T_2 & \cdots & T_{N-1} & T_N \\ T_1 & T_2 & \cdots & T_{N-1} & T_N \\ \cdots\\ T_1 & T_2 & \cdots & T_{N-1} & T_N \\ \end{array}\right)$$

  • each row in $\hat\Phi$ corresponds to one input sample ($10\times N$ ray traced references)
  • $N$ depends on the max degree $d$ as $N(d) = \binom{n+d}{d} = 4368$ (for 5 variables and degree $d=11$)
• standard procedure (linear least squares), but the matrix is too large for our taste!

finding a sparse polynomial

• use orthogonal matching pursuit [TG07]
• iteratively select most important columns in $\hat\Phi$

• original just looks for largest impact on residual (fast)
• we got better results by re-fitting all coefficents $c$ of all previously selected columns in the inner loop (somewhat slower)
• details see the paper

finding a sparse polynomial

• use orthogonal matching pursuit [TG07]
• iteratively select most important columns in $\hat\Phi$

  $$ \hat\Phi\cdot\mathbf{c} = \left(\begin{array}{cccc} T_1 & T_3 & \cdots & T_N \\ T_1 & T_3 & \cdots & T_N \\ \cdots\\ T_1 & T_3 & \cdots & T_N \\ \end{array}\right)\cdot \left(\begin{array}{c} c_1\\ c_3\\ .\\ c_N \end{array}\right)\approx\mathbf{O} $$

• we use up to 40 coefficients per equation (out of 4368 for degree 11)
• works transparently for aspheric and anamorphic lens elements
  • in particular no analytic Taylor expansion required!
• we also fit Fresnel transmittance $\tau$ to support coatings

aperture sampling via 2-step Newton iteration

• initial guess: straight on optical axis
• aperture error $\Rightarrow$ update sensor direction
• error in outgoing direction $\Rightarrow$ update sensor position

results: aperture sampling for light tracing (512spp)

results: aperture sampling for light tracing (closeup)